Schwarzschild check

import numpy as np
import matplotlib.pyplot as plt
import sympy as sp

# Import the module
import aurel
from aurel.solutions import Schwarzschild_isotropic as sol

L = 10
nt = 0.0
NRerror = []
NKerror = []
NNerror = []
allN = [32, 64, 96, 128, 144, 192]
for N in allN:
    print(" *** N = ", N)
    dx = 2*L / N
    param = { 'Nx': N, 'Ny': N, 'Nz': N, 
            'xmin': -L+0.01, 'ymin': -L+0.01, 'zmin': -L+0.01, 
            'dx': dx, 'dy': dx, 'dz': dx}
    fd = aurel.FiniteDifference(param, fd_order=8)
    rel = aurel.AurelCore(fd)
    rel.data = sol.data(nt, fd.x, fd.y, fd.z)
    rel.freeze_data()
    rel.memory_threshold_inGB = 20

    R_numerical = rel["s_RicciS"]
    Rerror = abs(R_numerical)
    NRerror += [np.nanmedian(fd.excision2(Rerror))]

    K_numerical = rel["Kretschmann"]
    K_exact = sol.Kretschmann(nt, fd.x, fd.y, fd.z)
    Kerror = abs((K_numerical - K_exact) / K_exact)
    NKerror += [np.nanmedian(fd.excision2(Kerror))]

    N_numerical = rel["null_ray_exp_out"]
    N_exact = sol.null_ray_exp_out(nt, fd.x, fd.y, fd.z)
    Nerror = abs((N_numerical - N_exact) / N_exact)
    NNerror += [np.nanmedian(fd.excision2(Nerror))]
    
    if N != allN[-1]:
        del fd, rel

 *** N =  32
8th order finite difference schemes are defined

Cosmological constant set to AurelCore.Lambda = 0.00e+00
Calculated gammaup3: $\gamma^{ij}$ Spatial metric with spatial indices up
Calculated s_Gamma_udd3: ${}^{(3)}{\Gamma^{k}}_{ij}$ Christoffel symbols of spatial metric with mixed spatial indices
Calculated s_Ricci_down3: ${}^{(3)}R_{ij}$ Ricci tensor of spatial metric with spatial indices down
Calculated s_RicciS: ${}^{(3)}R$ Ricci scalar of spatial metric
Calculated s_Riemann_uddd3: ${}^{(3)}{R^{i}}_{jkl}$ Riemann tensor of spatial metric with mixed spatial indices
Calculated s_Riemann_down3: ${}^{(3)}R_{ijkl}$ Riemann tensor of spatial metric with all spatial indices down
Calculated betax: $\beta^{x}$ x component of the shift vector with indices up. I assume $\beta^{x}=0$, if not then please define AurelCore.data['betax'] = ... 
Calculated betay: $\beta^{y}$ y component of the shift vector with indices up. I assume $\beta^{y}=0$, if not then please define AurelCore.data['betay'] = ... 
Calculated betaz: $\beta^{z}$ z component of the shift vector with indices up. I assume $\beta^{z}=0$, if not then please define AurelCore.data['betaz'] = ... 
Calculated betaup3: $\beta^{i}$ Shift vector with spatial indices up
Calculated betadown3: $\beta_{i}$ Shift vector with spatial indices down
Calculated gdown4: $g_{\mu\nu}$ Spacetime metric with spacetime indices down
Calculated gup4: $g^{\mu\nu}$ Spacetime metric with spacetime indices up
Calculated st_Ricci_down3: ${}^{(4)}R_{ij}$ Ricci tensor of spacetime metric with spatial indices down
Calculated Ktrace: $K = \gamma^{ij}K_{ij}$ Trace of extrinsic curvature
Calculated st_Riemann_down4: ${}^{(4)}R_{\alpha\beta\mu\nu}$ Riemann tensor of spacetime metric with spacetime indices down
Calculated st_Riemann_uudd4: ${}^{(4)}{R^{\alpha\beta}}_{\mu\nu}$ Riemann tensor of spacetime metric with mixed spacetime indices
Calculated Kretschmann: $K={R^{\alpha\beta}}_{\mu\nu}{R_{\alpha\beta}}^{\mu\nu}$ Kretschmann scalar
Calculated null_ray_exp_out: $\Theta_{out}$ List of expansion of null rays radially going out
 *** N =  64
8th order finite difference schemes are defined

Cosmological constant set to AurelCore.Lambda = 0.00e+00
Calculated gammaup3: $\gamma^{ij}$ Spatial metric with spatial indices up
Calculated s_Gamma_udd3: ${}^{(3)}{\Gamma^{k}}_{ij}$ Christoffel symbols of spatial metric with mixed spatial indices
Calculated s_Ricci_down3: ${}^{(3)}R_{ij}$ Ricci tensor of spatial metric with spatial indices down
Calculated s_RicciS: ${}^{(3)}R$ Ricci scalar of spatial metric
Calculated s_Riemann_uddd3: ${}^{(3)}{R^{i}}_{jkl}$ Riemann tensor of spatial metric with mixed spatial indices
Calculated s_Riemann_down3: ${}^{(3)}R_{ijkl}$ Riemann tensor of spatial metric with all spatial indices down
Calculated betax: $\beta^{x}$ x component of the shift vector with indices up. I assume $\beta^{x}=0$, if not then please define AurelCore.data['betax'] = ... 
Calculated betay: $\beta^{y}$ y component of the shift vector with indices up. I assume $\beta^{y}=0$, if not then please define AurelCore.data['betay'] = ... 
Calculated betaz: $\beta^{z}$ z component of the shift vector with indices up. I assume $\beta^{z}=0$, if not then please define AurelCore.data['betaz'] = ... 
Calculated betaup3: $\beta^{i}$ Shift vector with spatial indices up
Calculated betadown3: $\beta_{i}$ Shift vector with spatial indices down
Calculated gdown4: $g_{\mu\nu}$ Spacetime metric with spacetime indices down
Calculated gup4: $g^{\mu\nu}$ Spacetime metric with spacetime indices up
Calculated st_Ricci_down3: ${}^{(4)}R_{ij}$ Ricci tensor of spacetime metric with spatial indices down
Calculated Ktrace: $K = \gamma^{ij}K_{ij}$ Trace of extrinsic curvature
Calculated st_Riemann_down4: ${}^{(4)}R_{\alpha\beta\mu\nu}$ Riemann tensor of spacetime metric with spacetime indices down
Calculated st_Riemann_uudd4: ${}^{(4)}{R^{\alpha\beta}}_{\mu\nu}$ Riemann tensor of spacetime metric with mixed spacetime indices
Calculated Kretschmann: $K={R^{\alpha\beta}}_{\mu\nu}{R_{\alpha\beta}}^{\mu\nu}$ Kretschmann scalar
Calculated null_ray_exp_out: $\Theta_{out}$ List of expansion of null rays radially going out
 *** N =  96
8th order finite difference schemes are defined

Cosmological constant set to AurelCore.Lambda = 0.00e+00
Calculated gammaup3: $\gamma^{ij}$ Spatial metric with spatial indices up
Calculated s_Gamma_udd3: ${}^{(3)}{\Gamma^{k}}_{ij}$ Christoffel symbols of spatial metric with mixed spatial indices
Calculated s_Ricci_down3: ${}^{(3)}R_{ij}$ Ricci tensor of spatial metric with spatial indices down
Calculated s_RicciS: ${}^{(3)}R$ Ricci scalar of spatial metric
Calculated s_Riemann_uddd3: ${}^{(3)}{R^{i}}_{jkl}$ Riemann tensor of spatial metric with mixed spatial indices
Calculated s_Riemann_down3: ${}^{(3)}R_{ijkl}$ Riemann tensor of spatial metric with all spatial indices down
Calculated betax: $\beta^{x}$ x component of the shift vector with indices up. I assume $\beta^{x}=0$, if not then please define AurelCore.data['betax'] = ... 
Calculated betay: $\beta^{y}$ y component of the shift vector with indices up. I assume $\beta^{y}=0$, if not then please define AurelCore.data['betay'] = ... 
Calculated betaz: $\beta^{z}$ z component of the shift vector with indices up. I assume $\beta^{z}=0$, if not then please define AurelCore.data['betaz'] = ... 
Calculated betaup3: $\beta^{i}$ Shift vector with spatial indices up
Calculated betadown3: $\beta_{i}$ Shift vector with spatial indices down
Calculated gdown4: $g_{\mu\nu}$ Spacetime metric with spacetime indices down
Calculated gup4: $g^{\mu\nu}$ Spacetime metric with spacetime indices up
Calculated st_Ricci_down3: ${}^{(4)}R_{ij}$ Ricci tensor of spacetime metric with spatial indices down
Calculated Ktrace: $K = \gamma^{ij}K_{ij}$ Trace of extrinsic curvature
Calculated st_Riemann_down4: ${}^{(4)}R_{\alpha\beta\mu\nu}$ Riemann tensor of spacetime metric with spacetime indices down
Calculated st_Riemann_uudd4: ${}^{(4)}{R^{\alpha\beta}}_{\mu\nu}$ Riemann tensor of spacetime metric with mixed spacetime indices
Calculated Kretschmann: $K={R^{\alpha\beta}}_{\mu\nu}{R_{\alpha\beta}}^{\mu\nu}$ Kretschmann scalar
Calculated null_ray_exp_out: $\Theta_{out}$ List of expansion of null rays radially going out
 *** N =  128
8th order finite difference schemes are defined

Cosmological constant set to AurelCore.Lambda = 0.00e+00
Calculated gammaup3: $\gamma^{ij}$ Spatial metric with spatial indices up
Calculated s_Gamma_udd3: ${}^{(3)}{\Gamma^{k}}_{ij}$ Christoffel symbols of spatial metric with mixed spatial indices
Calculated s_Ricci_down3: ${}^{(3)}R_{ij}$ Ricci tensor of spatial metric with spatial indices down
Calculated s_RicciS: ${}^{(3)}R$ Ricci scalar of spatial metric
Calculated s_Riemann_uddd3: ${}^{(3)}{R^{i}}_{jkl}$ Riemann tensor of spatial metric with mixed spatial indices
Calculated s_Riemann_down3: ${}^{(3)}R_{ijkl}$ Riemann tensor of spatial metric with all spatial indices down
Calculated betax: $\beta^{x}$ x component of the shift vector with indices up. I assume $\beta^{x}=0$, if not then please define AurelCore.data['betax'] = ... 
Calculated betay: $\beta^{y}$ y component of the shift vector with indices up. I assume $\beta^{y}=0$, if not then please define AurelCore.data['betay'] = ... 
Calculated betaz: $\beta^{z}$ z component of the shift vector with indices up. I assume $\beta^{z}=0$, if not then please define AurelCore.data['betaz'] = ... 
Calculated betaup3: $\beta^{i}$ Shift vector with spatial indices up
Calculated betadown3: $\beta_{i}$ Shift vector with spatial indices down
Calculated gdown4: $g_{\mu\nu}$ Spacetime metric with spacetime indices down
Calculated gup4: $g^{\mu\nu}$ Spacetime metric with spacetime indices up
Calculated st_Ricci_down3: ${}^{(4)}R_{ij}$ Ricci tensor of spacetime metric with spatial indices down
Calculated Ktrace: $K = \gamma^{ij}K_{ij}$ Trace of extrinsic curvature
Calculated st_Riemann_down4: ${}^{(4)}R_{\alpha\beta\mu\nu}$ Riemann tensor of spacetime metric with spacetime indices down
Calculated st_Riemann_uudd4: ${}^{(4)}{R^{\alpha\beta}}_{\mu\nu}$ Riemann tensor of spacetime metric with mixed spacetime indices
Calculated Kretschmann: $K={R^{\alpha\beta}}_{\mu\nu}{R_{\alpha\beta}}^{\mu\nu}$ Kretschmann scalar
Calculated null_ray_exp_out: $\Theta_{out}$ List of expansion of null rays radially going out
 *** N =  144
8th order finite difference schemes are defined

Cosmological constant set to AurelCore.Lambda = 0.00e+00
Calculated gammaup3: $\gamma^{ij}$ Spatial metric with spatial indices up
Calculated s_Gamma_udd3: ${}^{(3)}{\Gamma^{k}}_{ij}$ Christoffel symbols of spatial metric with mixed spatial indices
Calculated s_Ricci_down3: ${}^{(3)}R_{ij}$ Ricci tensor of spatial metric with spatial indices down
Calculated s_RicciS: ${}^{(3)}R$ Ricci scalar of spatial metric
Calculated s_Riemann_uddd3: ${}^{(3)}{R^{i}}_{jkl}$ Riemann tensor of spatial metric with mixed spatial indices
Calculated s_Riemann_down3: ${}^{(3)}R_{ijkl}$ Riemann tensor of spatial metric with all spatial indices down
Calculated betax: $\beta^{x}$ x component of the shift vector with indices up. I assume $\beta^{x}=0$, if not then please define AurelCore.data['betax'] = ... 
Calculated betay: $\beta^{y}$ y component of the shift vector with indices up. I assume $\beta^{y}=0$, if not then please define AurelCore.data['betay'] = ... 
Calculated betaz: $\beta^{z}$ z component of the shift vector with indices up. I assume $\beta^{z}=0$, if not then please define AurelCore.data['betaz'] = ... 
Calculated betaup3: $\beta^{i}$ Shift vector with spatial indices up
Calculated betadown3: $\beta_{i}$ Shift vector with spatial indices down
Calculated gdown4: $g_{\mu\nu}$ Spacetime metric with spacetime indices down
Calculated gup4: $g^{\mu\nu}$ Spacetime metric with spacetime indices up
Calculated st_Ricci_down3: ${}^{(4)}R_{ij}$ Ricci tensor of spacetime metric with spatial indices down
Calculated Ktrace: $K = \gamma^{ij}K_{ij}$ Trace of extrinsic curvature
Calculated st_Riemann_down4: ${}^{(4)}R_{\alpha\beta\mu\nu}$ Riemann tensor of spacetime metric with spacetime indices down
Calculated st_Riemann_uudd4: ${}^{(4)}{R^{\alpha\beta}}_{\mu\nu}$ Riemann tensor of spacetime metric with mixed spacetime indices
Calculated Kretschmann: $K={R^{\alpha\beta}}_{\mu\nu}{R_{\alpha\beta}}^{\mu\nu}$ Kretschmann scalar
Calculated null_ray_exp_out: $\Theta_{out}$ List of expansion of null rays radially going out
 *** N =  192
8th order finite difference schemes are defined

Cosmological constant set to AurelCore.Lambda = 0.00e+00
Calculated gammaup3: $\gamma^{ij}$ Spatial metric with spatial indices up
Calculated s_Gamma_udd3: ${}^{(3)}{\Gamma^{k}}_{ij}$ Christoffel symbols of spatial metric with mixed spatial indices
Calculated s_Ricci_down3: ${}^{(3)}R_{ij}$ Ricci tensor of spatial metric with spatial indices down
Calculated s_RicciS: ${}^{(3)}R$ Ricci scalar of spatial metric
Calculated s_Riemann_uddd3: ${}^{(3)}{R^{i}}_{jkl}$ Riemann tensor of spatial metric with mixed spatial indices
Calculated s_Riemann_down3: ${}^{(3)}R_{ijkl}$ Riemann tensor of spatial metric with all spatial indices down
Calculated betax: $\beta^{x}$ x component of the shift vector with indices up. I assume $\beta^{x}=0$, if not then please define AurelCore.data['betax'] = ... 
Calculated betay: $\beta^{y}$ y component of the shift vector with indices up. I assume $\beta^{y}=0$, if not then please define AurelCore.data['betay'] = ... 
Calculated betaz: $\beta^{z}$ z component of the shift vector with indices up. I assume $\beta^{z}=0$, if not then please define AurelCore.data['betaz'] = ... 
Calculated betaup3: $\beta^{i}$ Shift vector with spatial indices up
Calculated betadown3: $\beta_{i}$ Shift vector with spatial indices down
Calculated gdown4: $g_{\mu\nu}$ Spacetime metric with spacetime indices down
Calculated gup4: $g^{\mu\nu}$ Spacetime metric with spacetime indices up
Calculated st_Ricci_down3: ${}^{(4)}R_{ij}$ Ricci tensor of spacetime metric with spatial indices down
Calculated Ktrace: $K = \gamma^{ij}K_{ij}$ Trace of extrinsic curvature
Calculated st_Riemann_down4: ${}^{(4)}R_{\alpha\beta\mu\nu}$ Riemann tensor of spacetime metric with spacetime indices down
CLEAN-UP: Cleaning up cache after 16 calculations...
CLEAN-UP: data size before cleanup: 29700.00 MB
CLEAN-UP: Removing cached value for 's_Ricci_down3' used 6 calculations ago (size: 486.00 MB).
CLEAN-UP: Removing cached value for 's_Riemann_uddd3' used 11 calculations ago (size: 4374.00 MB).
CLEAN-UP: Removing cached value for 's_Riemann_down3' used 10 calculations ago (size: 4374.00 MB).
CLEAN-UP: Removing cached value for 'gdown4' used 4 calculations ago (size: 864.00 MB).
CLEAN-UP: Removing cached value for 'gup4' used 2 calculations ago (size: 864.00 MB).
CLEAN-UP: Removed 5 items
CLEAN-UP: data size after cleanup: 18738.00 MB
Calculated gdown4: $g_{\mu\nu}$ Spacetime metric with spacetime indices down
Calculated gup4: $g^{\mu\nu}$ Spacetime metric with spacetime indices up
Calculated st_Riemann_uudd4: ${}^{(4)}{R^{\alpha\beta}}_{\mu\nu}$ Riemann tensor of spacetime metric with mixed spacetime indices
CLEAN-UP: Cleaning up cache after 19 calculations...
CLEAN-UP: data size before cleanup: 34290.00 MB
CLEAN-UP: Removing cached value for 'gammaup3' used 5 calculations ago (size: 486.00 MB).
CLEAN-UP: Removing cached value for 'st_Ricci_down3' used 5 calculations ago (size: 486.00 MB).
CLEAN-UP: Removing cached value for 'st_Riemann_down4' used 3 calculations ago (size: 13824.00 MB).
CLEAN-UP: Removing cached value for 'gdown4' used 2 calculations ago (size: 864.00 MB).
CLEAN-UP: Removed 4 items
CLEAN-UP: data size after cleanup: 18630.00 MB
Calculated Kretschmann: $K={R^{\alpha\beta}}_{\mu\nu}{R_{\alpha\beta}}^{\mu\nu}$ Kretschmann scalar
CLEAN-UP: Cleaning up cache after 20 calculations...
CLEAN-UP: data size before cleanup: 18684.00 MB
CLEAN-UP: Removing cached value for 'gup4' used 2 calculations ago (size: 864.00 MB).
CLEAN-UP: Removed 1 items
CLEAN-UP: data size after cleanup: 17820.00 MB
Calculated null_ray_exp_out: $\Theta_{out}$ List of expansion of null rays radially going out

plt.figure()

plt.loglog(allN, NRerror, 'o-', color='C0', label='3 Ricci scalar')
order = 8
ical = -3
converge = [NRerror[ical]*((allN[ical]/allN[i])**(order))for i in range(len(allN))]
plt.loglog(allN, converge, '--', color='C0', label='{}th order'.format(order))

plt.loglog(allN, NKerror, 'o-', color='C1', label='Kretschmann')
order = 8
ical = -3
converge = [NKerror[ical]*((allN[ical]/allN[i])**(order))for i in range(len(allN))]
plt.loglog(allN, converge, '--', color='C1', label='{}th order'.format(order))

plt.loglog(allN, NNerror, 'o-', color='C2', label=r'$\Theta_{out}$')
order = 8
ical = -3
converge = [NNerror[ical]*((allN[ical]/allN[i])**(order))for i in range(len(allN))]
plt.loglog(allN, converge, '--', color='C2', label='{}th order'.format(order))

plt.grid()
plt.xlabel('N')
plt.ylabel('Error')
plt.legend()
plt.title('8th order FD with excision')

Text(0.5, 1.0, '8th order FD with excision')
../_images/149306eae6146b0220677aa1839c93808d08e52b8bdd94156d6aaa2cd684de94.png

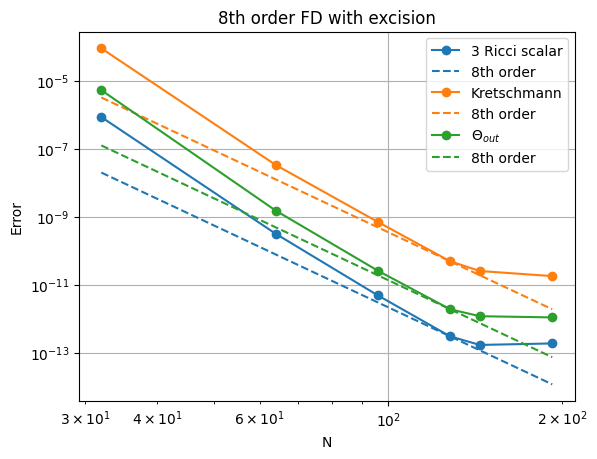
This shows better than 8th order convergence and a transition from truncation error (from the finite differencing) to floating point noise (from the number of digits stored).