Analytic check
import matplotlib.pyplot as plt
import numpy as np
import scipy.special as sc
import sympy as sp
import aurel
#from aurel.solutions import Collins_Stewart as sol
#from aurel.solutions import Conformally_flat as sol
from aurel.solutions import Harvey_Tsoubelis as sol
#from aurel.solutions import Non_diagonal as sol
#from aurel.solutions import Rosquist_Jantzen as sol
#from aurel.solutions import Schwarzschild as sol #too long for analytics
#from aurel.solutions import Szekeres as sol #too long for analytics
#Analytical setup
t, x, y, z = sp.symbols('t x y z')
# Spacetime
g = sol.gdown4(t, x, y, z, analytical=True)
an4 = aurel.AurelCoreSymbolic([t, x, y, z])
an4.data['gdown'] = g
# Space
gamma = sol.gammadown3(t, x, y, z, analytical=True)
an3 = aurel.AurelCoreSymbolic([x, y, z])
an3.data['gdown'] = gamma
# Numerical setup
L = 20
N = 64
grid = {
'Nx': N, # Number of data points per side
'Ny': N,
'Nz': N,
'xmin': - L / 2 + 0.01, # Minimum x coordinate
'ymin': - L / 2 + 0.01, # Minimum y coordinate
'zmin': - L / 2 + 0.01, # Minimum z coordinate
'dx': L / N, # Elementary grid size
'dy': L / N,
'dz': L / N,
}
fd = aurel.FiniteDifference(grid, boundary='other', fd_order=8)
rel = aurel.AurelCore(fd) # Need to pass Lambda=sol.Lambda if != 0.0
nt = 1
nx, ny, nz = fd.cartesian_coords
rel.data = sol.data(nt, nx, ny, nz)
rel.freeze_data()
8th order finite difference schemes are defined
Cosmological constant set to AurelCore.Lambda = 0.00e+00
err_max = 1e-4
custom_funcs = {
"hyper": lambda a, b, z: sc.hyp2f1(a[0], a[1], b[0], z), "exp_polar": np.exp
}
def compare_values(theory, numerical):
"""Compare analytical and numerical values, returning the maximum error.
Args:
theory: Analytical expression (SymPy).
numerical: Numerical array (NumPy).
Returns
-------
error: Maximum relative error (float).
"""
f_num = sp.lambdify((t, x, y, z), theory, modules=[custom_funcs, "numpy"])
s1 = np.real(f_num(nt, fd.cutoffmask(nx), fd.cutoffmask(ny), fd.cutoffmask(nz)))
s2 = fd.cutoffmask(numerical)
if theory != 0:
rel_err = np.abs(aurel.maths.safe_division(s2 - s1, s1))
error = np.max(np.ma.masked_invalid(rel_err))
else:
error = np.max(np.abs(s2))
return error
def checks(var, theory, numerical):
"""Print error information for a variable if above threshold.
Args:
var: Variable name (str).
theory: Analytical value.
numerical: Numerical value.
"""
error = compare_values(theory, numerical)
if error > err_max:
print(var,
", max(abs(num_val)) = ", np.max(abs(fd.cutoffmask(numerical))),
", relative error =", error)
def check1d(dim, var, theory, numerical):
"""Check 1D arrays element-wise and print errors above threshold.
Args:
dim: Dimension size (int).
var: Variable name (str).
theory: Analytical array.
numerical: Numerical array.
"""
for i in range(dim):
checks(var+f"{i}", theory[i], numerical[i])
def check2d(dim, var, theory, numerical):
"""Check 2D arrays element-wise and print errors above threshold.
Args:
dim: Dimension size (int).
var: Variable name (str).
theory: Analytical array.
numerical: Numerical array.
"""
for i in range(dim):
for j in range(dim):
checks(var+f"{i}{j}", theory[i, j], numerical[i, j])
def check3d(dim, var, theory, numerical):
"""Check 3D arrays element-wise and print errors above threshold.
Args:
dim: Dimension size (int).
var: Variable name (str).
theory: Analytical array.
numerical: Numerical array.
"""
for i in range(dim):
for j in range(dim):
for k in range(dim):
checks(var+f"{i}{j}{k}", theory[i, j, k], numerical[i, j, k])
def check4d(dim, var, theory, numerical):
"""Check 4D arrays element-wise and print errors above threshold.
Args:
dim: Dimension size (int).
var: Variable name (str).
theory: Analytical array.
numerical: Numerical array.
"""
for i in range(dim):
for j in range(dim):
for k in range(dim):
for h in range(dim):
checks(var+f"{i}{j}{k}{h}", theory[i, j, k, h], numerical[i, j, k, h])
def plot_them(analytical, numerical, cutoff=True):
"""Plot analytical vs numerical results and their relative error.
Args:
analytical: Analytical expression (SymPy).
numerical: Numerical array (NumPy).
cutoff: Whether to apply cutoff mask (bool, default True).
"""
f_num = sp.lambdify((t, x, y, z), analytical, modules=[custom_funcs, "numpy"])
A = np.real(f_num(nt, nx, ny, nz))
if isinstance(A, int) or isinstance(A, float):
A = np.full_like(numerical, A)
rel_error = np.abs(aurel.maths.safe_division(numerical - A, A))
ix, iy, iz = np.where(rel_error == np.max(rel_error))
if len(ix) > 1:
ix = ix[0]
iy = iy[0]
iz = iz[0]
print(f"max {np.max(rel_error):.2e} error at", ix, iy, iz)
if iy < 2*fd.mask_len or iz < 2*fd.mask_len:
cutoff = False
print('Max relative difference in boundary region')
if cutoff:
xv = fd.cutoffmask(fd.xarray)
nv = fd.cutoffmask(numerical[:,iy,iz])
av = fd.cutoffmask(A[:,iy,iz])
rv = fd.cutoffmask(rel_error[:,iy,iz])
else:
xv = fd.xarray
nv = numerical[:,iy,iz]
av = A[:,iy,iz]
rv = rel_error[:,iy,iz]
plt.figure()
plt.subplot(211)
plt.plot(xv, nv,
label="numerical")
plt.plot(xv, av,
linestyle='--',
label="analytical")
plt.grid()
plt.legend()
plt.subplot(212)
plt.semilogy(xv, rv)
plt.grid()
plt.ylabel("relative difference")
plt.xlabel("x")
plt.subplots_adjust(hspace=0.0)
Check Christoffel symbols
3D
check2d(3, "gamma^", an3["gup"], rel["gammaup3"])
check3d(3, "Γudd", an3["Gamma_udd"], rel["s_Gamma_udd3"])
Calculated symbolic gup: Metric tensor in the up index form
Calculated gammaup3: $\gamma^{ij}$ Spatial metric with spatial indices up
Calculated symbolic Gamma_udd: Christoffel symbols in the up-down-down index form
Calculated s_Gamma_udd3: ${}^{(3)}{\Gamma^{k}}_{ij}$ Christoffel symbols of spatial metric with mixed spatial indices
Γudd022 , max(abs(num_val)) = 208116.36229624215 , relative error = 0.0016382525191416827
Γudd202 , max(abs(num_val)) = 4.723738844061859 , relative error = 0.0001341854370830323
Γudd220 , max(abs(num_val)) = 4.723738844061859 , relative error = 0.0001341854370830323
4D
check2d(4, "g^", an4["gup"], rel["gup4"])
check3d(4, "Γudd", an4["Gamma_udd"], rel["st_Gamma_udd4"])
Calculated symbolic gup: Metric tensor in the up index form
Calculated alpha: $\alpha$ Lapse. I assume $\alpha=1$, if not then please define AurelCore.data['alpha'] = ...
Calculated betax: $\beta^{x}$ x component of the shift vector with indices up. I assume $\beta^{x}=0$, if not then please define AurelCore.data['betax'] = ...
Calculated betay: $\beta^{y}$ y component of the shift vector with indices up. I assume $\beta^{y}=0$, if not then please define AurelCore.data['betay'] = ...
Calculated betaz: $\beta^{z}$ z component of the shift vector with indices up. I assume $\beta^{z}=0$, if not then please define AurelCore.data['betaz'] = ...
Calculated betaup3: $\beta^{i}$ Shift vector with spatial indices up
Calculated betadown3: $\beta_{i}$ Shift vector with spatial indices down
Calculated betamag: $\beta_{i}\beta^{i}$ Magnitude of shift vector
Calculated gtt: $g_{tt}$ Metric with tt indices down.
Calculated gdown4: $g_{\mu\nu}$ Spacetime metric with spacetime indices down
Calculated gup4: $g^{\mu\nu}$ Spacetime metric with spacetime indices up
Calculated symbolic Gamma_udd: Christoffel symbols in the up-down-down index form
Calculated dtalpha: $\partial_t \alpha$ Coordinate time derivative of the lapse. I assume $\partial_t \alpha=0$, if not then please define AurelCore.data['dtalpha'] = ...
Calculated dtbetax: $\partial_t\beta^{x}$ Coordinate time derivative of the x component of the shift vector with indices up. I assume $\partial_t\beta^{x}=0$, if not then please define AurelCore.data['dtbetax'] = ...
Calculated dtbetay: $\partial_t\beta^{y}$ Coordinate time derivative of the y component of the shift vector with indices up. I assume $\partial_t\beta^{y}=0$, if not then please define AurelCore.data['dtbetay'] = ...
Calculated dtbetaz: $\partial_t\beta^{z}$ Coordinate time derivative of the z component of the shift vector with indices up. I assume $\partial_t\beta^{z}=0$, if not then please define AurelCore.data['dtbetaz'] = ...
Calculated dtbetaup3: $\partial_t\beta^{i}$ Coordinate time derivative of the shift vector with spatial indices up
Calculated st_Gamma_udd4: ${}^{(4)}{\Gamma^{\alpha}}_{\mu\nu}$ Christoffel symbols of spacetime metric with mixed spacetime indices
Γudd133 , max(abs(num_val)) = 208116.36229624215 , relative error = 0.0016382525191416827
Γudd313 , max(abs(num_val)) = 4.723738844061859 , relative error = 0.0001341854370830323
Γudd331 , max(abs(num_val)) = 4.723738844061859 , relative error = 0.0001341854370830323
Check Riemann and Ricci
3D
# Compute 3-Riemann tensor: R^i_{jkl}
check4d(3, "Ruddd", an3["Riemann_uddd"], rel["s_Riemann_uddd3"])
Calculated symbolic Riemann_uddd: Riemann curvature tensor in the up-down-down-down index form
Calculated s_Riemann_uddd3: ${}^{(3)}{R^{i}}_{jkl}$ Riemann tensor of spatial metric with mixed spatial indices
Ruddd0101 , max(abs(num_val)) = 0.016679485081112944 , relative error = 0.016679485081112944
Ruddd0102 , max(abs(num_val)) = 2331.4100690063497 , relative error = 0.0001242683747693139
Ruddd0110 , max(abs(num_val)) = 0.016679485081303968 , relative error = 0.016679485081303968
Ruddd0120 , max(abs(num_val)) = 2331.4100690063483 , relative error = 0.000124268374769899
Ruddd0201 , max(abs(num_val)) = 2331.4100690064515 , relative error = 0.00012426837472562759
Ruddd0202 , max(abs(num_val)) = 44052.60137026294 , relative error = 0.00014654071619464928
Ruddd0210 , max(abs(num_val)) = 2331.41006900645 , relative error = 0.00012426837472621268
Ruddd0220 , max(abs(num_val)) = 44052.601370262935 , relative error = 0.00014654071619464928
Ruddd1001 , max(abs(num_val)) = 4.372981885582807 , relative error = 0.0006823536802762492
Ruddd1010 , max(abs(num_val)) = 4.372981885582807 , relative error = 0.0006823536802762492
Ruddd1112 , max(abs(num_val)) = 0.08309351022762712 , relative error = 0.08309351022762712
Ruddd1121 , max(abs(num_val)) = 0.08309351022762712 , relative error = 0.08309351022762712
Ruddd1212 , max(abs(num_val)) = 0.7117688893340528 , relative error = 0.7117688893340528
Ruddd1221 , max(abs(num_val)) = 0.7117688893340528 , relative error = 0.7117688893340528
Ruddd2001 , max(abs(num_val)) = 0.5003281227507504 , relative error = 0.0006562455015008961
Ruddd2010 , max(abs(num_val)) = 0.5003281227507504 , relative error = 0.0006562455015008961
Ruddd2112 , max(abs(num_val)) = 0.00983646171152941 , relative error = 0.00983646171152941
Ruddd2121 , max(abs(num_val)) = 0.00983646171152941 , relative error = 0.00983646171152941
Ruddd2212 , max(abs(num_val)) = 0.08309351032949053 , relative error = 0.08309351032949053
Ruddd2221 , max(abs(num_val)) = 0.08309351032949053 , relative error = 0.08309351032949053
# Lower the first index: R_{lijk} = γ_{lm} R^m_{ijk}
check4d(3, "R_", an3["Riemann_down"], rel["s_Riemann_down3"])
Calculated symbolic Riemann_down: Riemann curvature tensor in the down index form
Calculated s_Riemann_down3: ${}^{(3)}R_{ijkl}$ Riemann tensor of spatial metric with all spatial indices down
CLEAN-UP: Cleaning up cache after 20 calculations...
CLEAN-UP: data size before cleanup: 694.00 MB
CLEAN-UP: Removing cached value for 'gammaup3' used 3 calculations ago (size: 18.00 MB).
CLEAN-UP: Removing cached value for 'betadown3' used 10 calculations ago (size: 6.00 MB).
CLEAN-UP: Removing cached value for 'gdown4' used 9 calculations ago (size: 32.00 MB).
CLEAN-UP: Removing cached value for 'gup4' used 8 calculations ago (size: 32.00 MB).
CLEAN-UP: Removing cached value for 'st_Gamma_udd4' used 2 calculations ago (size: 128.00 MB).
CLEAN-UP: Removed 5 items
CLEAN-UP: data size after cleanup: 478.00 MB
R_0101 , max(abs(num_val)) = 0.016679485081112944 , relative error = 0.016679485081112944
R_0102 , max(abs(num_val)) = 2331.4100690063497 , relative error = 0.0001242683747693139
R_0110 , max(abs(num_val)) = 0.016679485081303968 , relative error = 0.016679485081303968
R_0120 , max(abs(num_val)) = 2331.4100690063483 , relative error = 0.000124268374769899
R_0201 , max(abs(num_val)) = 2331.4100690064515 , relative error = 0.00012426837472562759
R_0202 , max(abs(num_val)) = 44052.60137026294 , relative error = 0.00014654071619464928
R_0210 , max(abs(num_val)) = 2331.41006900645 , relative error = 0.00012426837472621268
R_0220 , max(abs(num_val)) = 44052.601370262935 , relative error = 0.00014654071619464928
R_1001 , max(abs(num_val)) = 0.01412428077706889 , relative error = 0.01412428077706889
R_1002 , max(abs(num_val)) = 2331.913775963813 , relative error = 0.00016553528610018482
R_1010 , max(abs(num_val)) = 0.01412428077488208 , relative error = 0.01412428077488208
R_1020 , max(abs(num_val)) = 2331.913775963813 , relative error = 0.00016553528610103156
R_1212 , max(abs(num_val)) = 45.87134798262318 , relative error = 45.87134798262318
R_1221 , max(abs(num_val)) = 45.87134798262318 , relative error = 45.87134798262318
R_2001 , max(abs(num_val)) = 2331.68195273488 , relative error = 0.0013380956155417867
R_2010 , max(abs(num_val)) = 2331.681952734861 , relative error = 0.0013380956155319642
R_2112 , max(abs(num_val)) = 45.87135528560006 , relative error = 45.87135528560006
R_2121 , max(abs(num_val)) = 45.87135528560006 , relative error = 45.87135528560006
check2d(3, "R_", an3["Ricci_down"], rel["s_Ricci_down3"])
Calculated symbolic Ricci_down: Ricci curvature tensor in the down index form
Calculated gammaup3: $\gamma^{ij}$ Spatial metric with spatial indices up
Calculated s_Ricci_down3: ${}^{(3)}R_{ij}$ Ricci tensor of spatial metric with spatial indices down
R_00 , max(abs(num_val)) = 1.003148449103068 , relative error = 0.003148449103067996
R_11 , max(abs(num_val)) = 0.026515946792642336 , relative error = 0.026515946792642336
R_12 , max(abs(num_val)) = 2331.326975496122 , relative error = 0.00015990482733364868
R_21 , max(abs(num_val)) = 2331.326975496122 , relative error = 0.00015990482733364868
R_22 , max(abs(num_val)) = 44051.88960137361 , relative error = 0.00020066236838926717
checks("R", an3["RicciS"], rel["s_RicciS"])
Calculated symbolic RicciS: Ricci scalar
Calculated s_RicciS: ${}^{(3)}R$ Ricci scalar of spatial metric
R , max(abs(num_val)) = 2.0054514864455992 , relative error = 0.002725743222799615
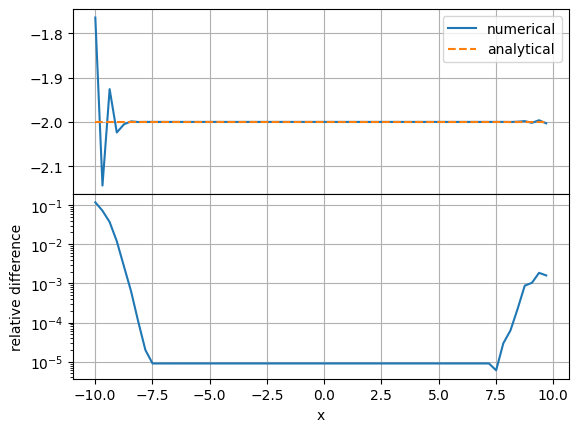
plot_them(an3["RicciS"], rel["s_RicciS"])
max 1.18e-01 error at [0] [0] [0]
Max relative difference in boundary region
4D
check4d(4, "Ruddd", an4["Riemann_uddd"], rel["st_Riemann_uddd4"])
Calculated symbolic Riemann_uddd: Riemann curvature tensor in the up-down-down-down index form
Calculated betadown3: $\beta_{i}$ Shift vector with spatial indices down
Calculated gdown4: $g_{\mu\nu}$ Spacetime metric with spacetime indices down
Calculated gup4: $g^{\mu\nu}$ Spacetime metric with spacetime indices up
Calculated Ktrace: $K = \gamma^{ij}K_{ij}$ Trace of extrinsic curvature
Calculated st_Ricci_down3: ${}^{(4)}R_{ij}$ Ricci tensor of spacetime metric with spatial indices down
Calculated st_Riemann_down4: ${}^{(4)}R_{\alpha\beta\mu\nu}$ Riemann tensor of spacetime metric with spacetime indices down
Calculated st_Riemann_uddd4: ${}^{(4)}{R^{\alpha}}_{\beta\mu\nu}$ Riemann tensor of spacetime metric with mixed spacetime indices
Ruddd0101 , max(abs(num_val)) = 0.0031484491030582262 , relative error = 0.0031484491030582262
Ruddd0110 , max(abs(num_val)) = 0.0031484491030582262 , relative error = 0.0031484491030582262
Ruddd0123 , max(abs(num_val)) = 0.01262044790564687 , relative error = 0.01262044790564687
Ruddd0132 , max(abs(num_val)) = 0.01262044790564687 , relative error = 0.01262044790564687
Ruddd0203 , max(abs(num_val)) = 19697.40712642635 , relative error = 0.0003891806778538999
Ruddd0230 , max(abs(num_val)) = 19697.40712642635 , relative error = 0.0003891806778538999
Ruddd0302 , max(abs(num_val)) = 19697.40712642635 , relative error = 0.0003891806778538999
Ruddd0303 , max(abs(num_val)) = 164064.5758265376 , relative error = 0.00020820998017207775
Ruddd0312 , max(abs(num_val)) = 19697.00558478495 , relative error = 0.000601699148547393
Ruddd0313 , max(abs(num_val)) = 164058.73499428353 , relative error = 0.0001017379136592247
Ruddd0320 , max(abs(num_val)) = 19697.40712642635 , relative error = 0.0003891806778538999
Ruddd0321 , max(abs(num_val)) = 19697.00558478495 , relative error = 0.000601699148547393
Ruddd0330 , max(abs(num_val)) = 164064.5758265376 , relative error = 0.00020820998017207775
Ruddd0331 , max(abs(num_val)) = 164058.73499428353 , relative error = 0.0001017379136592247
Ruddd1001 , max(abs(num_val)) = 0.0031484491030582262 , relative error = 0.0031484491030582262
Ruddd1010 , max(abs(num_val)) = 0.0031484491030582262 , relative error = 0.0031484491030582262
Ruddd1023 , max(abs(num_val)) = 0.01262044790564687 , relative error = 0.01262044790564687
Ruddd1032 , max(abs(num_val)) = 0.01262044790564687 , relative error = 0.01262044790564687
Ruddd1203 , max(abs(num_val)) = 19697.00558478495 , relative error = 0.000601699148547393
Ruddd1213 , max(abs(num_val)) = 19697.32403291621 , relative error = 0.00039339925765970705
Ruddd1230 , max(abs(num_val)) = 19697.00558478495 , relative error = 0.000601699148547393
Ruddd1231 , max(abs(num_val)) = 19697.32403291621 , relative error = 0.0003933992576816906
Ruddd1303 , max(abs(num_val)) = 164058.73499428353 , relative error = 0.0001017379136592247
Ruddd1312 , max(abs(num_val)) = 19697.32403291611 , relative error = 0.00039339925763772355
Ruddd1313 , max(abs(num_val)) = 164063.8640576504 , relative error = 0.00015205262380855634
Ruddd1321 , max(abs(num_val)) = 19697.32403291611 , relative error = 0.00039339925765970705
Ruddd1330 , max(abs(num_val)) = 164058.73499428353 , relative error = 0.0001017379136592247
Ruddd1331 , max(abs(num_val)) = 164063.8640576504 , relative error = 0.00015205262380855634
Ruddd2002 , max(abs(num_val)) = 0.5003766011970541 , relative error = 0.004461712594083345
Ruddd2003 , max(abs(num_val)) = 8.740676153529426 , relative error = 0.0005113896423065301
Ruddd2020 , max(abs(num_val)) = 0.5003766011970541 , relative error = 0.004461712594083345
Ruddd2030 , max(abs(num_val)) = 8.740676153529426 , relative error = 0.0005113896423065301
Ruddd2103 , max(abs(num_val)) = 8.73999212532988 , relative error = 0.0002991099226462979
Ruddd2112 , max(abs(num_val)) = 0.5008153624203805 , relative error = 0.005963771165482301
Ruddd2113 , max(abs(num_val)) = 8.741538532811123 , relative error = 0.0004457114229562048
Ruddd2121 , max(abs(num_val)) = 0.5008153624203763 , relative error = 0.005963771165482301
Ruddd2130 , max(abs(num_val)) = 8.73999212532988 , relative error = 0.0002991099226462979
Ruddd2131 , max(abs(num_val)) = 8.741538532810669 , relative error = 0.0004457114229562048
Ruddd2223 , max(abs(num_val)) = 0.08309351007491746 , relative error = 0.08309351007491746
Ruddd2232 , max(abs(num_val)) = 0.08309351007491746 , relative error = 0.08309351007491746
Ruddd2301 , max(abs(num_val)) = 0.00020943222492908245 , relative error = 0.00020943222492908245
Ruddd2310 , max(abs(num_val)) = 0.00020943222492908245 , relative error = 0.00020943222492908245
Ruddd2323 , max(abs(num_val)) = 0.7117688877163798 , relative error = 0.7117688877163798
Ruddd2332 , max(abs(num_val)) = 0.7117688877163798 , relative error = 0.7117688877163798
Ruddd3002 , max(abs(num_val)) = 0.0002525336748191673 , relative error = 0.0002525336748191673
Ruddd3003 , max(abs(num_val)) = 0.5002037766096384 , relative error = 0.001041708533186636
Ruddd3020 , max(abs(num_val)) = 0.0002525336748191673 , relative error = 0.0002525336748191673
Ruddd3030 , max(abs(num_val)) = 0.5002037766096384 , relative error = 0.001041708533186636
Ruddd3112 , max(abs(num_val)) = 0.0003281227507435711 , relative error = 0.0003281227507435711
Ruddd3113 , max(abs(num_val)) = 0.5001665635203726 , relative error = 0.0008805607837963914
Ruddd3121 , max(abs(num_val)) = 0.0003281227507435711 , relative error = 0.0003281227507435711
Ruddd3131 , max(abs(num_val)) = 0.5001665635203228 , relative error = 0.0008805607837963914
Ruddd3223 , max(abs(num_val)) = 0.00983646169337686 , relative error = 0.00983646169337686
Ruddd3232 , max(abs(num_val)) = 0.00983646169337686 , relative error = 0.00983646169337686
Ruddd3323 , max(abs(num_val)) = 0.08309351014149692 , relative error = 0.08309351014149692
Ruddd3332 , max(abs(num_val)) = 0.08309351014149692 , relative error = 0.08309351014149692
check4d(4, "R_", an4["Riemann_down"], rel["st_Riemann_down4"])
Calculated symbolic Riemann_down: Riemann curvature tensor in the down index form
R_0101 , max(abs(num_val)) = 0.0031484491030582262 , relative error = 0.0031484491030582262
R_0110 , max(abs(num_val)) = 0.0031484491030582262 , relative error = 0.0031484491030582262
R_0123 , max(abs(num_val)) = 0.01262044790564687 , relative error = 0.01262044790564687
R_0132 , max(abs(num_val)) = 0.01262044790564687 , relative error = 0.01262044790564687
R_0203 , max(abs(num_val)) = 19697.40712642635 , relative error = 0.0003891806778538999
R_0230 , max(abs(num_val)) = 19697.40712642635 , relative error = 0.0003891806778538999
R_0302 , max(abs(num_val)) = 19697.40712642635 , relative error = 0.0003891806778538999
R_0303 , max(abs(num_val)) = 164064.5758265376 , relative error = 0.00020820998017207775
R_0312 , max(abs(num_val)) = 19697.00558478495 , relative error = 0.000601699148547393
R_0313 , max(abs(num_val)) = 164058.73499428353 , relative error = 0.0001017379136592247
R_0320 , max(abs(num_val)) = 19697.40712642635 , relative error = 0.0003891806778538999
R_0321 , max(abs(num_val)) = 19697.00558478495 , relative error = 0.000601699148547393
R_0330 , max(abs(num_val)) = 164064.5758265376 , relative error = 0.00020820998017207775
R_0331 , max(abs(num_val)) = 164058.73499428353 , relative error = 0.0001017379136592247
R_1001 , max(abs(num_val)) = 0.0031484491030582262 , relative error = 0.0031484491030582262
R_1010 , max(abs(num_val)) = 0.0031484491030582262 , relative error = 0.0031484491030582262
R_1023 , max(abs(num_val)) = 0.01262044790564687 , relative error = 0.01262044790564687
R_1032 , max(abs(num_val)) = 0.01262044790564687 , relative error = 0.01262044790564687
R_1203 , max(abs(num_val)) = 19697.00558478495 , relative error = 0.000601699148547393
R_1213 , max(abs(num_val)) = 19697.32403291621 , relative error = 0.00039339925765970705
R_1230 , max(abs(num_val)) = 19697.00558478495 , relative error = 0.000601699148547393
R_1231 , max(abs(num_val)) = 19697.32403291621 , relative error = 0.0003933992576816906
R_1303 , max(abs(num_val)) = 164058.73499428353 , relative error = 0.0001017379136592247
R_1312 , max(abs(num_val)) = 19697.32403291611 , relative error = 0.00039339925763772355
R_1313 , max(abs(num_val)) = 164063.8640576504 , relative error = 0.00015205262380855634
R_1321 , max(abs(num_val)) = 19697.32403291611 , relative error = 0.00039339925765970705
R_1330 , max(abs(num_val)) = 164058.73499428353 , relative error = 0.0001017379136592247
R_1331 , max(abs(num_val)) = 164063.8640576504 , relative error = 0.00015205262380855634
R_2003 , max(abs(num_val)) = 19697.40712642635 , relative error = 0.0003891806778538999
R_2030 , max(abs(num_val)) = 19697.40712642635 , relative error = 0.0003891806778538999
R_2103 , max(abs(num_val)) = 19697.00558478495 , relative error = 0.000601699148547393
R_2112 , max(abs(num_val)) = 2331.6857012733462 , relative error = 0.0002281854824960171
R_2113 , max(abs(num_val)) = 19696.820325958746 , relative error = 0.00039205847954967344
R_2121 , max(abs(num_val)) = 2331.6857012733462 , relative error = 0.0002281854824960171
R_2130 , max(abs(num_val)) = 19697.00558478495 , relative error = 0.000601699148547393
R_2131 , max(abs(num_val)) = 19696.820325958746 , relative error = 0.00039205847954967344
R_2301 , max(abs(num_val)) = 0.01262044790564687 , relative error = 0.01262044790564687
R_2310 , max(abs(num_val)) = 0.01262044790564687 , relative error = 0.01262044790564687
R_2323 , max(abs(num_val)) = 45.87134784460068 , relative error = 45.87134784460068
R_2332 , max(abs(num_val)) = 45.87134784460068 , relative error = 45.87134784460068
R_3002 , max(abs(num_val)) = 19697.40712642635 , relative error = 0.0003891806778538999
R_3003 , max(abs(num_val)) = 164064.5758265376 , relative error = 0.00020820998017207775
R_3012 , max(abs(num_val)) = 19697.00558478495 , relative error = 0.000601699148547393
R_3013 , max(abs(num_val)) = 164058.73499428353 , relative error = 0.0001017379136592247
R_3020 , max(abs(num_val)) = 19697.40712642635 , relative error = 0.0003891806778538999
R_3021 , max(abs(num_val)) = 19697.00558478495 , relative error = 0.000601699148547393
R_3030 , max(abs(num_val)) = 164064.5758265376 , relative error = 0.00020820998017207775
R_3031 , max(abs(num_val)) = 164058.73499428353 , relative error = 0.0001017379136592247
R_3103 , max(abs(num_val)) = 164058.73499428353 , relative error = 0.0001017379136592247
R_3112 , max(abs(num_val)) = 19697.0521491877 , relative error = 0.0006904520382722087
R_3113 , max(abs(num_val)) = 164059.24308140838 , relative error = 0.0001625071400577208
R_3121 , max(abs(num_val)) = 19697.0521491877 , relative error = 0.0006904520382722087
R_3130 , max(abs(num_val)) = 164058.73499428353 , relative error = 0.0001017379136592247
R_3131 , max(abs(num_val)) = 164059.24308140838 , relative error = 0.0001625071400577208
R_3201 , max(abs(num_val)) = 0.01262044790564687 , relative error = 0.01262044790564687
R_3210 , max(abs(num_val)) = 0.01262044790564687 , relative error = 0.01262044790564687
R_3223 , max(abs(num_val)) = 45.871355175971985 , relative error = 45.871355175971985
R_3232 , max(abs(num_val)) = 45.871355175971985 , relative error = 45.871355175971985
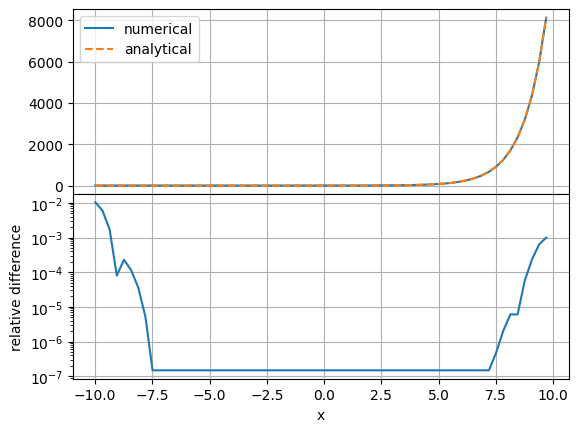
plot_them(an4["Riemann_down"][2,1,2,1], rel["st_Riemann_down4"][2,1,2,1])
max 1.04e-02 error at 0 1 0
Max relative difference in boundary region
check2d(4, "R_", an4["Ricci_down"], rel["st_Ricci_down4"])
Calculated symbolic Ricci_down: Ricci curvature tensor in the down index form
Calculated Ttrace: $T$ Trace of the energy-stress tensor
Calculated st_Ricci_down4: ${}^{(4)}R_{\alpha\beta}$ Ricci tensor of spacetime metric with spacetime indices down
checks("R", an4["RicciS"], rel["st_RicciS"])
Calculated symbolic RicciS: Ricci scalar
Calculated st_RicciS: ${}^{(4)}R$ Ricci scalar of spacetime metric